To calculate the net acceptance and efficiency for finding particles of interest we merged GEANT output for full central Au-Au collisions with shielding hits and with single particle events in which the species of interest was generated according to the model described above. Thus we can estimate not only the probability that the interesting particle makes it through the apparatus, but also the probability of finding the track in the presence of the other tracks in the event and tracks from interactions in the surrounding material.
Runs of this type were carried out for a few thousand each of several of the interesting
species at the appropriate settings of the spectrometer magnets.
Figure 
shows the reconstructed mass spectrum for a charge +1 mass 12 GeV/c 
object.
Some central protons are accepted by the detector and appear in the plot along
with the higher mass peak.
Figure shows the same plot with an expanded scale along with a Gaussian
fit to the peak. The parameters of the fit are given on the plot.
Figure: Reconstructed mass (GeV/c ) spectrum for events with a charge +1 mass
12 GeV/c object.
Figure: Reconstructed mass (GeV/c )spectrum for a charge +1 mass
12 GeV/c object. Solid curve is
a Gaussian fit to the peak.
Table gives the mass resolution, geometric acceptance and track
reconstruction efficiency for several species covering the range of Z/A
of interest at each of the magnetic
field settings we plan to use. Also shown is the product
of the acceptance times efficiency and the spectrometer magnetic field used. Both
spectrometer magnets are set to the same field for all runs.
The geometric acceptance of the apparatus is characterized by the acceptance in
rigidity parallel and perpendicular to the incident beam direction
( 
and 
). Table gives the acceptance in percent as a function
of and for the spectrometer field set to +1.5T (positive strangelet
search). For reference, a 10 GeV/ 
strangelet at center of
mass rapidity for 11.7 GeV/c Au-Au collisions has rigidity 25 GeV/c and average P 
of 1.9 GeV/c according to our model. As an example, Table shows the
acceptance as a function of P 
and rapidity for a 10 GeV charge +1 strangelet with
the spectrometer field set to +1.5T.
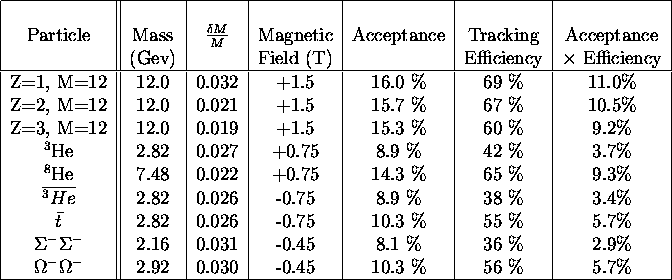
Table: Summary of Single Particle Acceptance and Tracking Efficiency
Table: Acceptance in percent as a function of parallel and perpendicular rigidity
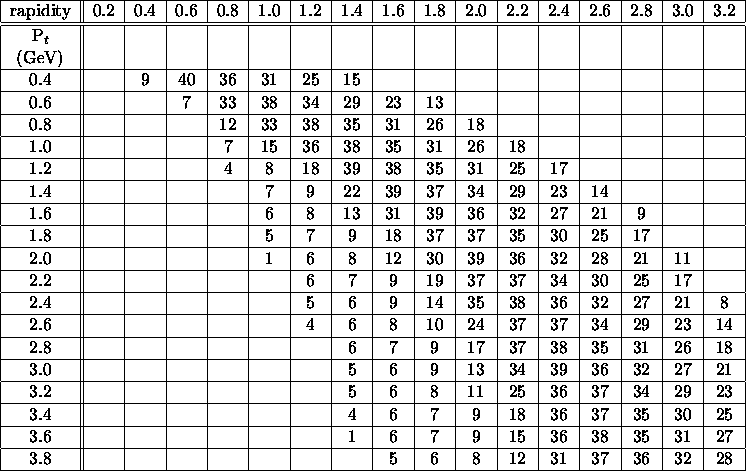
Table: Acceptance in percent for a 10 GeV charge +1 strangelet. The center of
mass rapidity for Au-Pb collisions is 1.59
We have varied the parameters ( 
) in the single particle generator
over a reasonable range and have found the acceptance to be relatively insensitive to
the details of the model. For example, varying 
from 0.5 to 0.9 changes the acceptance
by from 10 to 30% depending on the charge and mass of the state considered.
A comment is in order regarding the overall tracking efficiency. In order to achieve
very high background rejection redundant measurements are used. One must then
require that every detector have the correct signal to form a good track. This means
that, for example, if two particles strike a single hodoscope counter the vertical
position measured by that counter will be incorrect, and will not match the straw tube
hits. Both tracks will then be lost. We accept this inefficiency in order to
achieve high background rejection. As discussed above, we have studied the
optimization of scintillation counter sizes to minimize such losses. For more
abundant species, where the highest background rejection is not required, one can be
less stringent than requiring every detector to have the correct signal. Also, as a
possible upgrade, we could add multi-hit capability to the digitizers. We have not
assumed either of these however in calculating the efficiencies given in
Table .
For neutral particles, we use the same single particle model to calculate the
geometric acceptance. The efficiency for finding showers in the calorimeter
will be discussed below. Table gives the geometric
acceptance for neutral particles for several masses over the range of interest.
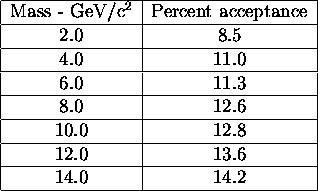
Table: Percent acceptance for neutral particles.