The calorimeter is the primary detector for the study of neutral particles. The flight times and energy deposits measured by the calorimeter are the basic data from which the masses of the incident particles are deduced. The hodoscopes and wire chambers will be used to identify charged particles incident on the calorimeter so that their signals will not be confused with those of neutrals.
We have not yet carried out a fully detailed Monte Carlo simulation
however we draw upon
experience with the E814 calorimeters to understand what may be
possible in E864. The E814 calorimeters have a tower geometry with
transverse dimensions of 20 cm (horizontally) by 10 cm (vertically).
The individual towers in E814's calorimeter do not have independent time
measurements, although the sum of all 12 towers in each vertical stack
have a time measurement with an r.m.s. error of about 1 ns.
The timing is not used in the E814 cluster-finding analysis.
By using the shower shapes two 
GeV neutrons can be distinguished if they
strike the calorimeter more than 5 cm from one another. To do this, a program
which uses a fast Monte Carlo as part of a chi-squared analysis of multi
neutron hypotheses is necessary. In this analysis the best one neutron
hypothesis (energy and impact point) is compared with the best two neutron
hypothesis, etc.
In E864 the tower geometry, good resolution, hermeticity, and excellent time resolution of the spaghetti design are essential ingredients for the neutral particle studies. It will be important to use the best possible analysis techniques to identify showers caused by the accidental overlap of several neutrons which can simulate higher mass particles. The E864 calorimeter will have 10 cm by 10 cm towers. Each individual tower will have a time measurement with an expected r.m.s. error of 0.5 ns or less. The TDC's attached to each tower will be ``single hit'' TDC's. Thus, if two neutrons hit a given tower, only the time for fastest will be recorded. This results in the two overlapping neutron events displaying a lower mass, on the average, than two neutron masses.
The most challenging task for the calorimeter is to detect a possible
signal from the H 
-dibaryon. Since the mass is expected to be slightly more than
twice the neutron mass there will be background from the resolution tail of
single neutrons and from overlapping double, triple, etc., neutrons.
For possible higher mass states, the background problems become less severe
as the mass increases. We focus the discussion below on the most
difficult task of detecting the H .
We estimate the background to the H as follows. A sample of
HIJET/GEANT central Au-Au collisions are traced through the tracking
system to the calorimeter. These events include all physics processes and tracks
from shielding interactions. From this sample of events we select all neutrons
entering the calorimeter which were late ( 
0.976) but would still fall
inside the ADC gates (TOF < 142 ns). These neutrons are then analyzed using
gaussian errors for the calorimeter energy and time of flight.
Single neutrons are analyzed under both the hypothesis that the calorimeter
energy is deposited by a neutron and that it is deposited by an H .
Figure 
shows a scatter plot of the two mass hypotheses
Figure: Scatter plot of reconstructed mass of particles interpreted
as neutrons and as H 's. Dots are for neutrons and open circles are H 's
assuming an RMS energy resolution 
and and RMS timing
resolution of 0.5 ns. Also shown in Fig. is a sample of
H 's (open circles) selected and reconstructed in the same manner. The H 's
are generated with a mass of 2 GeV/c 
according to the single particle
model described in the section on HIJET/GEANT. Although the scatter plot looks
encouraging for detecting the H 's, one must recall that the number of
neutrons striking the calorimeter is about 7 per
central event. The number of H 's per central event is about
0.1(acceptance - see Table ) 
. 
is
the production rate of H 's per central event and is expected to be
10 
to 10 
. From Fig. one can see that
the sum of the two mass hypotheses ( 
) will be an effective
discriminator between neutrons and H 's. Figure shows a histogram
of this quantity for single neutrons (solid) and H 's (dashed).
Figure: Histogram of sum of the two mass hypotheses (neutron and H )
for neutrons (solid) and H 's (dashed).
Clearly, to minimize background from single neutrons in
the H region it is necessary to have excellent resolution and to minimize
the high mass tail of the resolution. Figure shows the
Figure: Expected apparent mass of neutrons reconstructed as H 's as a
function of time of flight. Time for a v=c particle is subtracted.
expected apparent mass of neutrons reconstructed as H 's as a function
of time of flight (with time for a v=c particle subtracted). Also shown
is the effect of adding one standard deviation to the time of flight or
to the energy and the combined effect of both. As expected, for short
times (velocity near c), the time of flight error dominates the mass resolution.
For very slow particles, the shape of the curve brings the apparent mass closer
to the H mass. We clearly can have better separation of H 's and
neutrons by eliminating early and late times. Figure shows
the apparent mass of neutrons
Figure: Scatter plot shows the apparent mass of neutrons reconstructed as H 's
vs time of flight.
Figure: Histogram of the apparent mass of neutrons reconstructed as H 's.
with additional timing cuts.
reconstructed as H 's as a function of time of flight. Figure
shows a histogram of the apparent mass of neutrons reconstructed as H 's after applying
the additional timing cut: 95.5 < TOF < 110 ns (0.83 
0.96).
About 80% of the H 's pass
these cuts which are clearly useful in reducing the high mass tail from the neutrons
(compare Fig. with the single neutron spectrum in
Fig. ).
We will give a quantitative estimate of the single neutron background below, but
first we consider background from overlapping neutrons. We use the same sample
of central collisions described above, but now select pairs of neutrons that
fall within a certain distance of each other, or triplets of neutrons that
fall within a certain distance from the energy weighted centroid of the triplet.
In each of these cases the calorimeter energy for the pair or triplet is summed,
and the time of flight of the earliest neutron is assigned to this energy (the DA
system has single hit TDC's).
This system is then reconstructed as above under both the assumption of a
single neutron and an H . Figures and show
the spectrum of the sum of the two mass hypotheses
Figure: Sum of two mass hypotheses (neutron and H ) for two overlapping
neutrons
Figure: Sum of two mass hypotheses (neutron and H ) for three overlapping
neutrons
for pairs and triplets of neutrons using the timing cuts described for the single neutrons above.
To estimate the sensitivity we assume a 100 hour run using only the multiplicity
trigger. Such a run will record 2.88 
central collisions. We
actually plan two such runs - one with positive magnetic field and one with
negative field. The acceptance for neutrals will be the same in each run.
Table shows the number of reconstructed neutral showers expected from
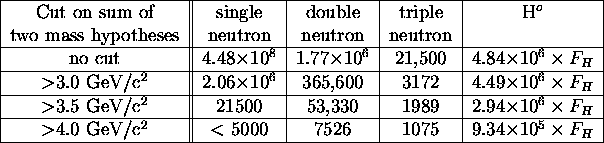
Table: Numbers of events from various sources for a 100 hour run.
Calorimeter energy resolution assumed to
be .
each source (single neutron, double neutron, triple neutron and H ) for
several different cuts on the sum of the two mass hypotheses (neutron or H ).
The number of H 's detected is a function of , the production rate of
H 's per central event. The timing cuts described above are used to
select these events. The number of double neutron events is calculated
assuming that a 4 cm minimum distance is required to identify two neutrons as
such and reject them. We have also included an efficiency of 42% for
finding good showers which pass shape cuts. From Table we
conclude that a statistically significant excess of events ( 
)
attributable to the H will be observed for H production rates as low
as 10 per central event. Table
shows the results of the same analysis assuming a calorimeter energy resolution
of 
. Under this assumption, the signal to noise is somewhat
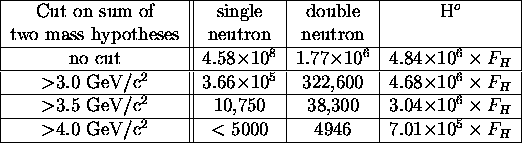
Table: Numbers of events from various sources for a 100 hour run.
Calorimeter energy resolution assumed to be .
improved for the lowest cut on the summed mass hypotheses so that one would expect
to see a statistically significant mass peak for H production rates as low
as 10 per central event. We also note that our studies show that the triple
neutron overlap background is not the dominant background source provided one can
eliminate triple neutron clusters where the neutron falling furthest from the
energy weighted centroid of the three is at least 10 cm from the centroid.
Another potential background source is due to antineutrons which could be
produced in these events. The production rate of the H is expected to
be comparable to the rate of antineutrons (based on antiproton
production data obtained in E802 and E814 for 14.5 GeV Si ions on
lead [48, 11]). Monte Carlo calculations
presented in the original E864 proposal show that there is considerable
overlap between H -dibaryons and antineutrons for a large fraction
of the kinematic regime of interest. However, E864 will have very
high statistics measurements of antiproton production. These measurements
will characterize not only the antiproton spectra but also the detector response
to antinucleons. With these data we should be able to adequately predict
the shape and magnitude of the antineutron background. Given the expectation
of similar rates for antineutrons and H -dibaryons and the high statistical
power of the data sample, we should be able to carry out the H search even in
the presence of significant antineutron background.
Several comments can be made about our sensitivity to the H :
is critically dependant
on the calorimeter resolution. This particular physics goal will be compromised
by reduced calorimeter performance. comes from
the very large event sample (Tables and ). With
such high statistics, we can afford to use a variety of cuts to enhance the
H signal. The high statistics also allows observation of a small signal on
a large background. we will have to use the most sophisticated
calorimeter analysis and also have the best possible understanding of the performance
of the calorimeter. Although the study presented above makes the simplistic
assumption of gaussian errors which may lead to under estimating the background,
it also does not take advantage of shape cuts (both in space and time) on the
towers involved in a shower. Such cuts should help eliminate multi-particle showers.
For particles of higher mass, the background becomes lower due to the
lower likelihood of more than three overlapping neutrons. There is also
a greater likelihood of one of the background neutrons revealing a wrong
time of flight. For particle masses of about 7 GeV/c , we expect
that the calorimeter rejection will be comparable to that found in the
analysis described for the charged particle case, i.e. a background rate
of about 10 
per central event. For masses greater than
7 GeV, the charged particle analysis ran out of statistics, but
given our overlap picture, it is reasonable to expect the background to
continue to fall as the mass of interest increases.
Extrapolating the background spectrum found in the charged particle case
indicates that the background drops by about a factor of 10 for each
additional 1.5 baryon masses added. We reiterate that the
calorimeter analysis used in the charged particle case was appreciably
cruder than that which will be used for the neutral analysis.