It is perhaps useful to map out the region of stability of strangelets
for a particular choice of the parameters 
in the
assumed Bethe-Weizacker mass formula. For illustration, we take
MeV, 
MeV, corresponding to
. We then obtain
The strangelet radius parameter is 
fm, corresponding to a
density twice that of nuclear matter.
One can now determine the region of (A,Y,Z) values for which
strangelets are stable with respect to both strong 
and weak
hadron emission.
In addition to neutron emission considered previously, we also
consider stability with respect to proton or 
emission.
Stability against proton emission sets a limit on the amount of
positive charge a strangelet may carry, while stability
constrains the amount of negative charge. The systems considered in
this example are all stable with respect to strong or weak 
and
emission. The Q values are given by
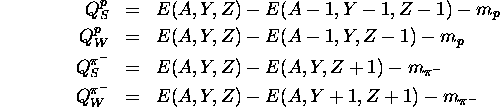
We then have
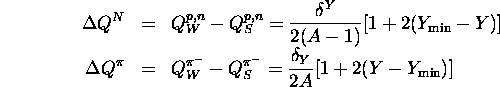
For 
, we have 
, whereas for
, 
; thus strong nucleon decay
dominates where 
becomes too small and strong pion decay
occurs when gets too large. Together, these decay
processes provide bounds on S and Z for stable strangelets of
fixed A. For example, the requirement of stability against
strong emission 
implies
with 
. Since 
and 
increases with A, the above condition does not permit
stable negatively charged strangelets for large A. However, in the
region of small 
which is probed by E864, a substantial
region of negatively charged stable strangelets is allowed. For our
example, we have stability for
Thus we arrive at an interesting conclusion: if we assume the form of
the Bethe-Weizacker mass formula given by the Bag Model, and
is small enough to yield a region of stability, then most
of the stable strangelets of small A will in fact be negatively
charged. Stated another way: for small A, the requirement of
stability against proton emission provides a rather stringent
restriction on positive Z, while emission allows a more
generous region of negative Z.
To illustrate the above observations, we consider the stability of
strangelets with A=7, for the choice MeV. The
condition of stability against proton emission rules out strangelets
with 
. For 
, the proton stability conditions play
no role, since they are less restrictive than those for neutron
emission. The allowed regime of stability with respect to both weak
and strong neutron and emission is shown in Table 
.
The lower bound on S comes from emission and the upper bound
from neutron emission. We include all entries for which the amount of
negative charge is limited by the condition 
, which characterizes systems composed of SU(3) octet baryons in the
hadron basis (no 
).
Inspection of Table discloses that there are 26 stable
objects predicted with A=7; of these, 17 are negatively charged.
Table: Regions of stability of an A=7 strangelet, with
MeV.
Of course, this zone of stability is very sensitive to our choice of
: as increases, the number of stable objects
decreases, and the region of stability moves to higher A.
The domain of stable A=7 systems with Z<0 is accessible to
E864, and the experimental backgrounds are less severe than for
Z>0. We now refine our previous estimates of coalescence rates to
include the Z dependence, in order to see which of these objects
might be observed by E864. For Z<0, the lightest hadronic
configuration which can coalesce to form the strangelet is composed of
n, and 
particles. Heavier configurations of
the same (A,Z,S), where 
is replaced by 
, are
neglected; they could also contribute to coalescence, but are further
``off-shell.''
The generalization of our previous estimate for the number of strangelets N per collision is
for Z<0, where P is the penalty factor for adding a neutron to a
cluster, 
is the penalty for converting a neutron to a
, and 
is the penalty for changing a
to (this builds up the negative charge). The
neutron-to-proton ratio for the Au-Au collision is 3/2; the factor
reflects the conversion of the two protons in the 
to neutrons. Using the values 
, 
,
, we arrive at 26 stable strangelets with A=7.
Of these, 18 have rates 
, and are thus likely to be
within the
sensitivity of E864. These 18 objects, along with their estimated
production rates,
are displayed in Table . Figure also
illustrates the stable A=7 strangelets, with the 18 detectable strangelets
circled.
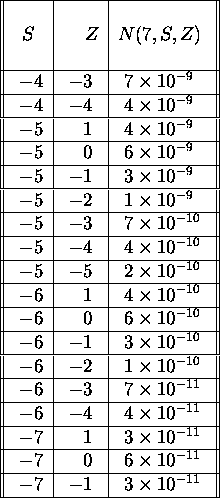
Table: Estimated number N of A=7 strangelets per Au-Au collision.
All are within E864's sensitivity.
Figure: The A=7 strangelets which are stable against strong and weak p,
n, and 
decay. The species which are likely to be accessible with
E864's sensitivity are shown by circled dots. We have assumed a Bethe-Weizacker
strangelet mass formula with MeV, MeV,
and estimated production rates with a simple coalescence model.
If the sensitivity of the experiment were to be decreased to the
level, 13 of the above species are still detectable, at the
level, 6 are detectable, and at the 
level, none
are accessible. The importance of very high sensitivity is thus
clear: the zone of stable and also detectable objects shrinks rather
quickly with decreasing sensitivity.
It is important to note that the objects produced with the highest
rate are near the boundary of the region of stability, in particular
those with minimum . In addition to the A=7
strangelets shown in Table , a few of the stable A=8,9
systems could also be detected by E864.
The above discussion was based on the existence of a Bethe-Weizacker
mass formula for strangelets, and the further assumption that the
parameters 
, 
, 
, and are
uniquely related to 
as in the Bag Model. In this
particular dynamical framework, E864 will serve to provide a lower
limit on the energy per particle of bulk strange matter,
if no strangelets are found, assuming that the coalescence model
estimates of production rates are reasonable.