The basic idea that a new form of matter, so-called strange quark matter, might exist and be stable against strong decay (or possibly even absolutely stable) has been suggested in Refs. [2, 3, 7]. The discovery of strange quark matter, or the determination of significant upper limits for its production rate, is a major goal of the proposed experiment. The ``new'' matter consists of multi quark states containing u, d, and s quarks in a single ``bag.'' In essence, the strangeness degree of freedom allows more quarks to occupy low lying levels than is possible with two flavors. This leads to the possibility that an assembly of baryon number, A, might be metastable or even stable when all of the quarks are in a single bag. This is in contrast to the case of ordinary nuclei where the quarks of a large A system are (mostly!) organized into 3 quark, color-neutral bags (the neutrons and protons) which interact with one another by meson exchange forces.
A mass formula of Bethe-Weizacker type for strangelets was developed in Ref. [23]. The energy E(A,Y,Z) of a strangelet of baryon number A, hypercharge Y=A+S (S = strangeness) and electric charge Z assumes the form
The two parameters of the theory are the energy per baryon
in bulk matter (large A) and the strange quark mass
. The most stable strangelets have (Y,Z) close to
( 
, 
).
The quantities of interest here, namely the regions of
where the system is stable with respect to weak and
strong neutron emission, are much more sensitive to than
. The strangelet surface tension, 
, radius parameter
, as well as the parameters 
, ,
, of the above Taylor expansion can all be
expressed in terms of and an angle 
defined by
In particular,
Typically, the strangelet density 
is of order
twice that of non-strange nuclear matter.
In weak or strong neutron emission from strangelets, respectively, the
energy releases 
are given by
The qualitative features of strangelet stability, as a function of
y=Y/A and A, for fixed 
MeV, 
MeV/c 
and
, are shown in Fig. 
, taken from Berger and
Jaffe [23]. For A=15, typical stability regions in the
(Z,Y) plane are indicated in Fig. , from Ref. [4]. As
increases towards the neutron mass 
, the region of
strong neutron decay marches to the left in Fig. , and
intersects the weak decay region, which marches to the right. If there is
a gap between the weak and strong decay regions, E864 would have the best
chance of finding a stable strangelet with 
and
, in the vicinity of the dot in Fig. . At AGS
energies, since the amount of strangeness produced is limited, the
region of stability for 
is
probably not accessible. For 
, the value of
is given roughly by
For MeV, the variation of with is
displayed in Table .
Figure: Strangelet stability as a function of Y and A for fixed
MeV, MeV/c , and . From
Ref. [23].
Figure: Stability regions in the (Z,Y) plane for an A=15 strangelet.
From Ref. [23].
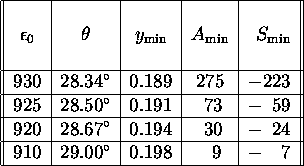
Table: The variation of with for MeV.
Note that , , and vary only weakly
with changes in , whereas and the associated
strangeness value 
are very sensitive
to .
There is clearly a limit to the amount of strangeness and baryon
number that we can assemble in a bound strangelet, starting with the
hadronic soup resulting from a central Au-Au collision. The
coalescence estimates presented later, although perhaps somewhat
conservative, suggest that composite strange clusters with 
might be formed with measurable rates in E864. Thus
if is too large, we cannot fabricate a cluster with
. Inspection of Table reveals that if
MeV, we are in the domain of sensitivity of
E864. Viewed in the context of an assumed Bethe-Weizacker mass
formula, the absence of a strangelet signal in E864 could be
translated into a constraint on the volume term .
The calculations based on the MIT Bag Model, which yield a
Bethe-Weizacker mass formula, are suggestive but clearly are not
definitive predictions. Since this approach is essentially a Taylor
series in 
, it is not reliable for small A. In
particular, it is unclear at what minimum value of A stable
strangelets 
occur. Farhi and Jaffe [7]
have done explicit quark shell model calculations for 
,
finding no stable strangelets (the H-dibaryon is a possible exception,
treated explicitly later). That perturbative calculation was based on
one-gluon exchange; multi-quark states with a high degree of symmetry may
become stable because of non-perturbative effects [24].
Thus one should properly regard the
possible existence of strange quark matter as a question to be
resolved by experiment.